Visualization is a very important aspect of problem-solving. To learn the order of operations visually, we will discuss substitution arithmetic today where we will use symbols to replace arithmetic operations. Let's get started with some examples.
In this example, we are using a ♡ as an arithmetic symbol. Why ♡? Because we want you to fall in love with math. If you remember, additions and subtractions were just symbols until someone told rules associated with those symbols. After a lot of practice, we figured out + sign means addition. Then we were asked to do additions by counting by two's, three's, etc. Once we started to count by two's and three's, we were told that it's nothing but multiplication. Addition suddenly became multiplication.
Key point is that there are standard rules of arithmetic which you already know but creative kids like you would like to make their own rules. No one can stop you from making your own rules and creating a parallel world of your own mathematics. Are you ready for it?
Let's slow down and learn to deal with the ♡s first. In the first example, ♡ is defining a relationship between a and b. When you have a + b then you add just one copy of a with one copy of b. ♡ is a very generous arithmetic operator defined by us. When we created this new arithmetic symbol ♡, we defined a rule with it. This rule is to add 3 copies of a with 4 copies of b which makes is a♡b = 3a + 4b.
Did you figure out value of 2♡3? I am sure you did. You are very smart. Can you please check our work below?
Thanks for checking. Let's try something else. 2 + 3 = 3 + 2. This is called Commutative Property. You can move a and b around freely without changing the results. I am sure you know it very well too.
Does Commutative Property hold true for our newly defined operator ♡? Is 2♡3 = 3♡2? What do you think? We don't like guesswork so let's figure it out by doing some work.
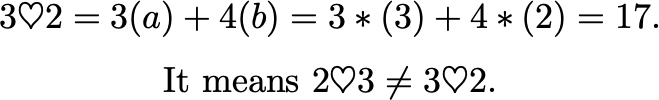
It's heartbreaking to see that this ♡ is not commutative. Having said that, we have a very big heart. We are going to define a new symbol that can follow the Commutative Property.
What do we need to do differently to define such a symbol? Why was a♡b not commutative? We noticed that coefficients of a and b were different for ♡ operations. Maybe that was the culprit. If we have a non-symmetric relationship, it may not be commutative.
Why don't we define a symbol with a symmetric relationship to confirm our hypothesis? Let's call this new symbol a spade - ♠.
Similar to the previous problem, we can solve: 2♠3 = 4*2 +4*3 = 20 and 3♠2 = 4*3 +4*2 = 20.
Symmetry made ♠ look very cool in this case. The key here is to understand that you have the power to define your own arithmetic operations. Remember, with great power comes great responsibilities. If you like programming and use it with this newly earned power, you may end up crashing your computer or servers but that's the way we learn. Never hesitate in experimenting as long as it is safe to do so.
Just like normal arithmetic operations, you can do series of operations using your own arithmetic symbols. Let's try the following example.
As one ♡ may not be enough to make you fall in love with math, we are using two ♡s in this problem. It makes this problem bit complicated but we know that you love challenges.
What should we do next to solve this problem? Can we apply the order of operations here i.e. solve brackets first?
Now we can replace value of 3♡4 in (-5)♡(3♡4):
So far we learned the power of defining our own arithmetic operations and use those to solve many interesting problems. With some practice, we can master the art of solving more complex problems. We can find many such problems in math competitions. Hopefully, this was helpful to make you fall in love with math.
Here are few more problems for you to try:
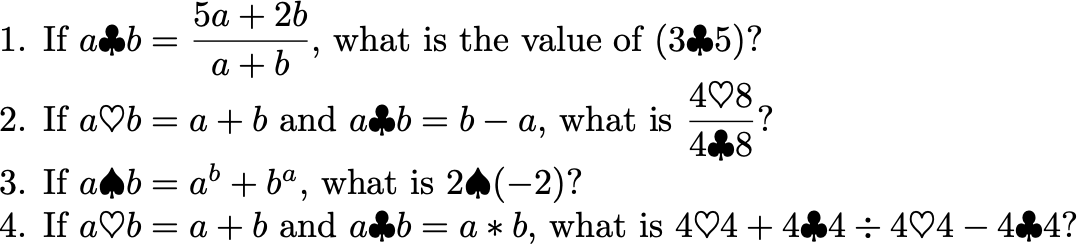
If you would like to try more questions like this, you can join Canadian Innovation Math Contest which is available to you for free. You may also win many amazing award.
More Math in Action


